代わりに入れる 連立方程式の解き方は\(2\) 種類です。 加減法と代入法です。 加減法はマスターしましたか? 続いて、連立方程式の解き方の2代入法を学習しましょう。 例題1 次の連立方程式を代入法で解きなさい。 $\left\{ \begin{array}{@{}1} 3xy=2\\ y=x4連立方程式代入法の解き方 次の連立方程式を解きなさい。 \begin{eqnarray} \left\{ \begin{array}{l} x = 2y8 \\ 2x 5y = 2 \end{array} \right \end{eqnarray}連立方程式の代入法の解き方 を解説していくよ。 よかったら参考にしてみてね^^ 連立方程式の代入法の解き方がわかる4つのステップ 例題といっしょに解説していくよ。 例題 つぎの連立方程式を代入法で解きなさい。 2x 3y = 14 3x y = 0
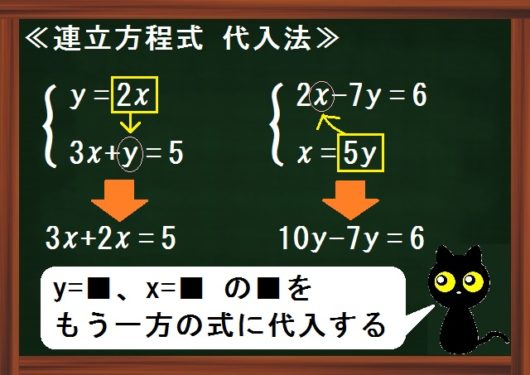
中学数学 連立方程式 の効果的な教え方 代入法
代入法 連立 方程式 解き方
代入法 連立 方程式 解き方-連立方程式(代入法1) 三平方の定理 難しい問題でもすぐに答を見ようとせず今までにやってきたことを思い出しながら解き方を考えましょう。代入法を用いた連立方程式の練習問題です。 解説記事はこちら gt;連立方程式代入法を使った問題の解き方は?やり方をイチから解説! スポンサーリンク 目次1 方程式練習問題連立方程式の代入法2 練習問題の解答&解



連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ
連立方程式の形が、どちらか一方でも式が \(x=\) もしくは \(y=\) という形になっている場合には代入法を使うとラクに解くことができます。1 上の連立1次方程式をGaussの消去法、GaussJordan法、LU分解法で解け。 2 上の連立1次方程式をJacobi法、GaussSeidel法、SOR法で解け。 3 本講義で解説した解法の中から一つ選び、プログラミングし動作確認せよ。 4 下の問題を3のプログラムを利用し解け。上記の3元連立方程式を例に取り進めていきます。 2a 2b 3c = 15 (1) 3a 5b 2c = 19 (2) 5a 3b 3c = (3) の解は、a=1,b=2,c=3ですが、 これは次のように表すこともできます。 1a 0b 0c = 1 (1)' 0a 1b 0c = 2 (2)' 0a 0b 1c = 3 (3)' そうすると、もし上の式から下の式に変換することが
加減法と代入法では、特に解き方が指定されていない場合は、どちらを用いて解いてもOKです。 自分の解きやすい方法で解けばいいでしょう 。 ・ 加減法:連立方程式の解き方対象:中1 中2 中3 ⭐️⭐️⭐️やる気スイッチを、入れませんか?⭐️⭐️⭐️ 個別指導学習塾スクールieはこんな学習塾です。 ・まずは独自の診断ツールであなたの性格と学力を分析します ・診断結果に基づいてあなたに合った講師を選びます ・世界に一冊、あなただけのオーダーメイド加減法と代入法では、特に解き方が指定されていない場合は、どちらを用いて解いてもOKです。 自分の解きやすい方法で解けばいいでしょう 。 ・ 加減法:連立方程式の解き方
連立方程式の代入法の解き方 を解説していくよ。 よかったら参考にしてみてね^^ 連立方程式の代入法の解き方がわかる4つのステップ 例題といっしょに解説していくよ。 例題 つぎの連立方程式を代入法で解きなさい。 2x 3y = 14 3x y = 01 上の連立1次方程式をGaussの消去法、GaussJordan法、LU分解法で解け。 2 上の連立1次方程式をJacobi法、GaussSeidel法、SOR法で解け。 3 本講義で解説した解法の中から一つ選び、プログラミングし動作確認せよ。 4 下の問題を3のプログラムを利用し解け。連立方程式の解き方には、 加減法 と 代入法 の2つの計算方法があります。どちらの解き方でも答えは同じになるので、解き方の指定がない場合には解きやすい方法で解けばいいかと思います。 加減法でも代入法でも解き方の考え方で共通しているのは方程



中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット
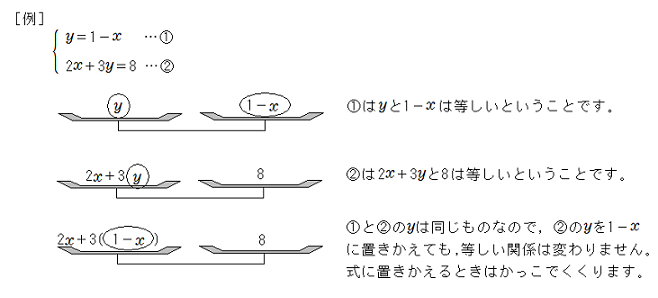


連立方程式 代入法を使った連立方程式の解き方 中学数学 定期テスト対策サイト
代入法を用いた連立方程式の練習問題です。 解説記事はこちら gt;連立方程式代入法を使った問題の解き方は?やり方をイチから解説! スポンサーリンク 目次1 方程式練習問題連立方程式の代入法2 練習問題の解答&解連立方程式 代入法 の解き方教えて下さい 問題は 2xy=8 2x=3y4 です学校で習っててよくわからなくて 自己流でやったらそっちでもあっていてそっちでおぼえていてもとのやり方を忘れました。連立方程式の代入法の解き方 を解説していくよ。 よかったら参考にしてみてね^^ 連立方程式の代入法の解き方がわかる4つのステップ 例題といっしょに解説していくよ。 例題 つぎの連立方程式を代入法で解きなさい。 2x 3y = 14 3x y = 0


連立方程式 加減法の問題と代入法の問題の解き方



Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
連立方程式の便利なところ 連立方程式の解き方には「加減法」「代入法」とありますが、解くだけなら代入法は必要ありません。 ⇒ 加減法とは?連立方程式の解き方とポイント しかし、図形(座標)上の意味を考えたとき、代入法の便利さがわかります。対象:中1 中2 中3 ⭐️⭐️⭐️やる気スイッチを、入れませんか?⭐️⭐️⭐️ 個別指導学習塾スクールieはこんな学習塾です。 ・まずは独自の診断ツールであなたの性格と学力を分析します ・診断結果に基づいてあなたに合った講師を選びます ・世界に一冊、あなただけのオーダーメイド「それじゃあ、無理矢理1と0にしちゃえー」、というのが行列を使った 連立方程式の解き方で、上で説明したものをより数学的に表したものです。 こういう行列的な計算方法は、Excelで視覚的に計算課程を見ていく方が 遙かにわかりやすいです。



連立方程式の2つの解き方 代入法 加減法 数学fun



連立方程式の代入法 簡単な問題で やり方をわかりやすく紹介 中学や高校の数学の計算問題
のような連立方程式を、 消去法で計算するとき、 のように、 「形」を見て、 「上と下の式を足して、y を消す」と、 先に決めてから計算します。 続きの計算は、省略します。 のような連立方程式を、 消去法で計算するとき、 のような「形」になるように、 「2つの式を変形する」と、 先に「連立方程式の解き方って、 "加減法・代入法"の 両方ができないとダメですか? 」 大丈夫、安心してください。 結論から言えば、 「自分の解きやすい方法」でOKです。 どちらの解き方も 同じ答え になるので、 "正しい答え"に どちらでも到達でき連立方程式の解き方には、 加減法 と 代入法 の2つの計算方法があります。どちらの解き方でも答えは同じになるので、解き方の指定がない場合には解きやすい方法で解けばいいかと思います。 加減法でも代入法でも解き方の考え方で共通しているのは方程



連立方程式の解き方 代入法 Youtube



中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
次の連立方程式を代入法で解きなさい。 \begin{eqnarray} (3)\begin{cases} 3y=154x ・・・① & \\ 2x3y=3 ・・・② & \end{cases} \end{eqnarray} STEP $\textcolor{blue}{1}$ :一方の式を他方の式に代入し、片方の文字を消去する $154x$ を②の式の $3y$ に代入代入法の解き方 まとめ お疲れ様でした! 代入法の解き方は簡単だったね(^^) 慣れてくれば 加減法よりも式が少ないし 楽に感じるのではないかと思います。 関数の単元で、連立方程式が必要になる場合には ほとんどが代入法で解いていくようになるから①代入法の問題の解き方。解き方は2通りある。 連立方程式における代入法は ①連立している2つの方程式のうち、どちらか一つをxまたはyについて解く。 つまり「x=」や「y=」の形に等式変形する。 ②こうして等式変形したものを、残った方の式に代入



連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ
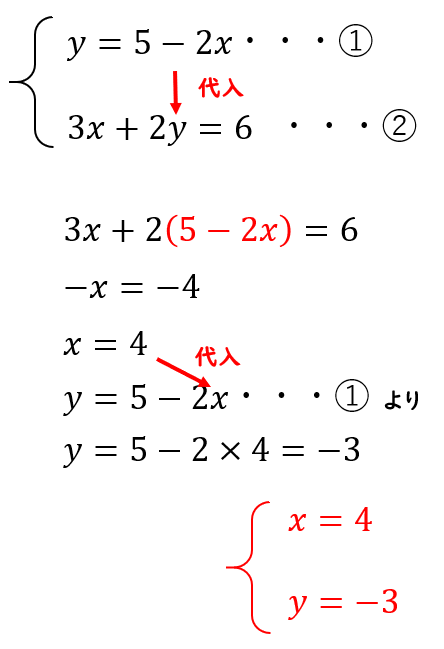


連立方程式の2つの解き方 代入法 加減法 数学fun
のような連立方程式を、 消去法で計算するとき、 のように、 「形」を見て、 「上と下の式を足して、y を消す」と、 先に決めてから計算します。 続きの計算は、省略します。 のような連立方程式を、 消去法で計算するとき、 のような「形」になるように、 「2つの式を変形する」と、 先に連立方程式を解く 連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に加減法と代入法がある。 加減法 x,またはyの係数をそろえて2つの式を 「たす」または「ひく」して文字を一つ消す。連立方程式(代入法1) 三平方の定理 難しい問題でもすぐに答を見ようとせず今までにやってきたことを思い出しながら解き方を考えましょう。



中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook



超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく



数学中2 連立方程式とその解き方 中学数学に関する質問 勉強質問サイト


連立方程式の代入法による解き方を勉強しています 添付の問題の Yahoo 知恵袋



2 連立方程式の解き方 代入法 やすこぶたの勉強部屋中2



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook



中学2年生 数学 無料問題集 連立方程式を代入法で解く おかわりドリル



連立方程式 代入法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト


第1章 連立方程式


中学2年 連立方程式代入法の問題が分かりません 写真の問題です Yを変形して Yahoo 知恵袋


連立方程式の解き方 Gains ゲインズ ネットスクールの資格取得応援情報サイト


代入法のやり方 連立方程式の問題で役に立つ解き方だぞ 三重の個人契約家庭教師
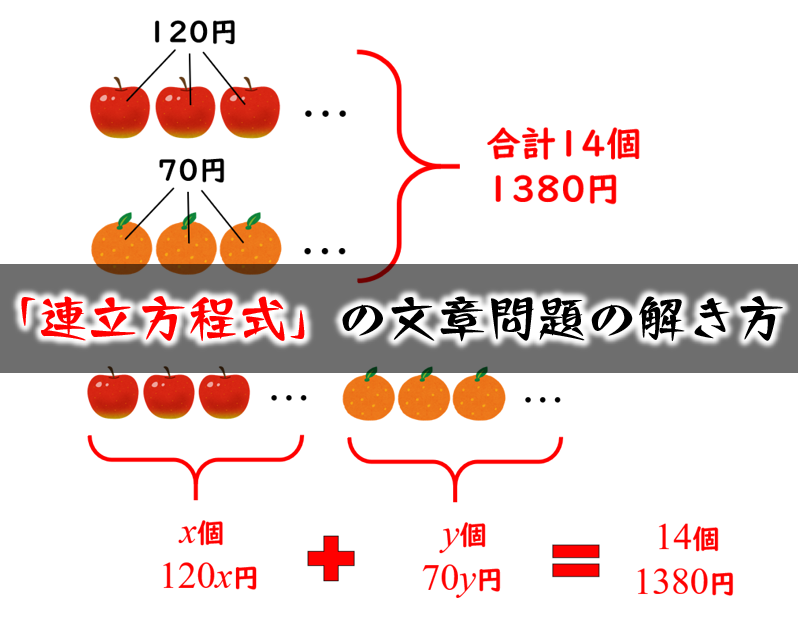


連立方程式の文章問題の解き方 数学fun


連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
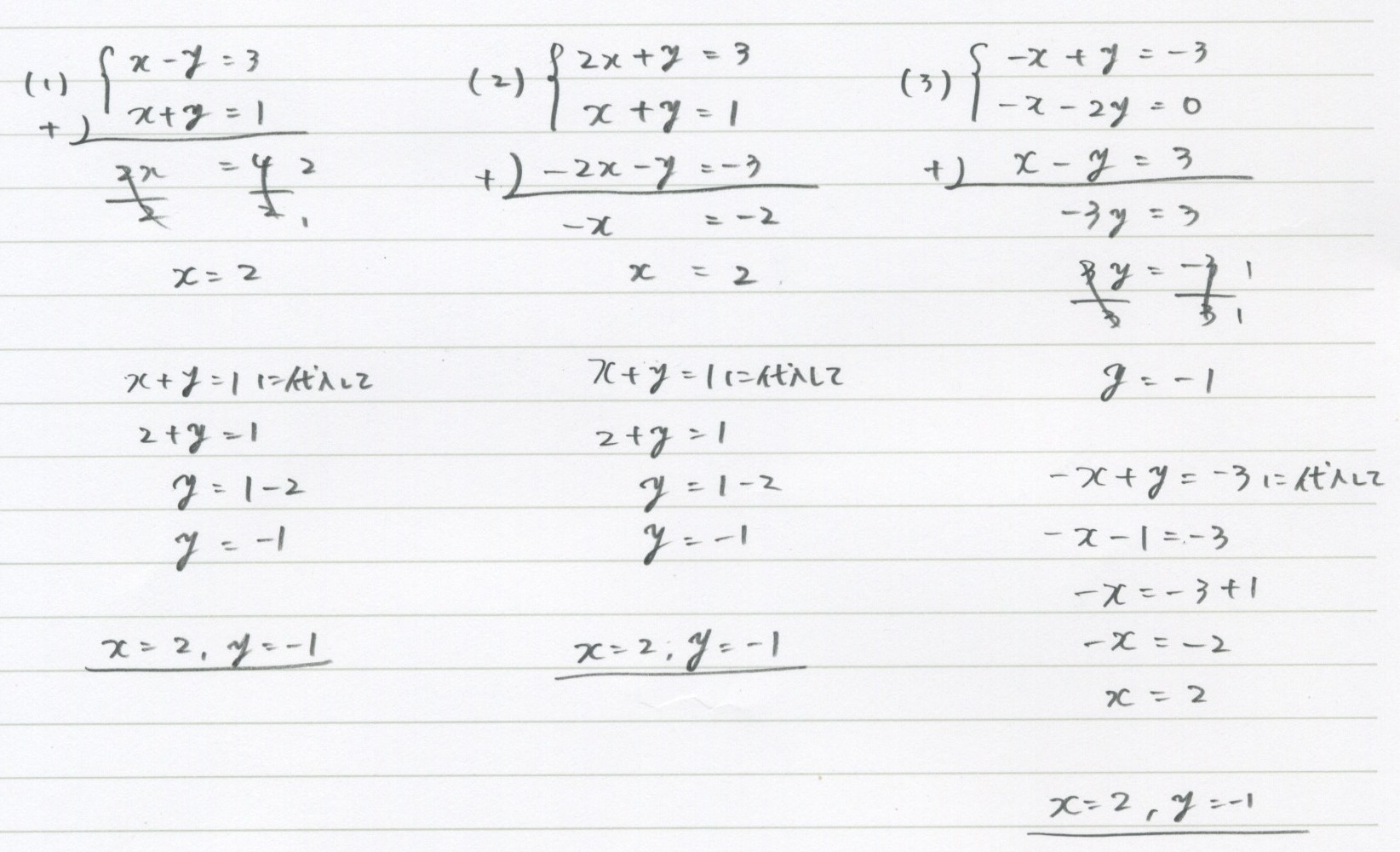


5 1 連立方程式 基本 勉強できようサイト



Junior High数学的中2数字 連立方程式 授業ノート 筆記 Clear



解き方 連立方程式の代入法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
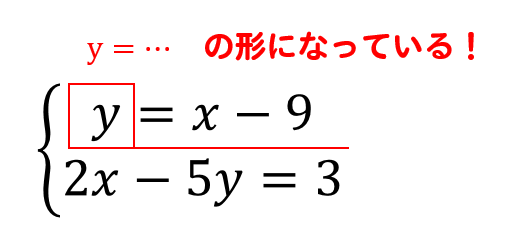


連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ



都立入試コラム第1弾 連立方程式の解き方 タダゼミ 杉並 大学生による無料の都立高校合格講座



連立方程式 代入法 無料で使える中学学習プリント



連立方程式 連立方程式の加減法と代入法 中学数学 定期テスト対策サイト


連立方程式 代入法2 チーム エン



連立方程式の代入法 問題の解き方は イチからやってみよう 中学数学 理科の学習まとめサイト



中学数学 中学2年 Vol 0 連立方程式の解き方 代入法 Youtube



連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ


この連立方程式の解き方を教えてもらいたいです 教えてもらう立場で図々し Yahoo 知恵袋



連立方程式を小学生に教える



3分でわかる 連立方程式の代入法と加減法をわかりやすく 合格サプリ



連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ


代入法とは 1分でわかる意味 連立方程式の解き方 代入法のやり方 移項 加減法との関係


連立方程式 代入法 頭の体操



連立方程式を小学生に教える



3分でわかる 連立方程式の代入法と加減法をわかりやすく 合格サプリ



連立方程式 1 代入法と加減法 バカでもわかる 中学数学



代入法による解き方 中2数学 連立方程式4 Youtube



子供向けぬりえ これまでで最高の連立 方程式 代入 法 解き方



連立方程式の解き方代入法1 中学数学 講義 Youtube


連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料


連立方程式



中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu



連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ
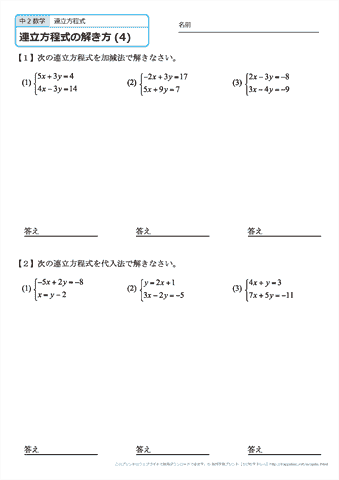


中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生


連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス



分数をふくむ連立方程式 Youtube



数学の連立方程式のやり方が分かりません 教えてくれると有難いです Clear



連立方程式の解き方 加減法 代入法と文章題の計算方法 リョースケ大学



中学数学 連立方程式 の効果的な教え方 代入法



Kistenkasten723 中2数学で連立方程式の解法として 最初に加減法 次に代入法を習う 画像は代入法を説明した直後の練習問題である 掛算 超算数 算数 算数教育 テスト 試験 文脈 さくらんぼ計算



中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu



代入法のやり方 連立方程式の問題で役に立つ解き方だぞ 三重の個人契約家庭教師



連立方程式の解き方 代入法 加減法による解法と勉強のポイント



解き方 連立方程式の代入法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
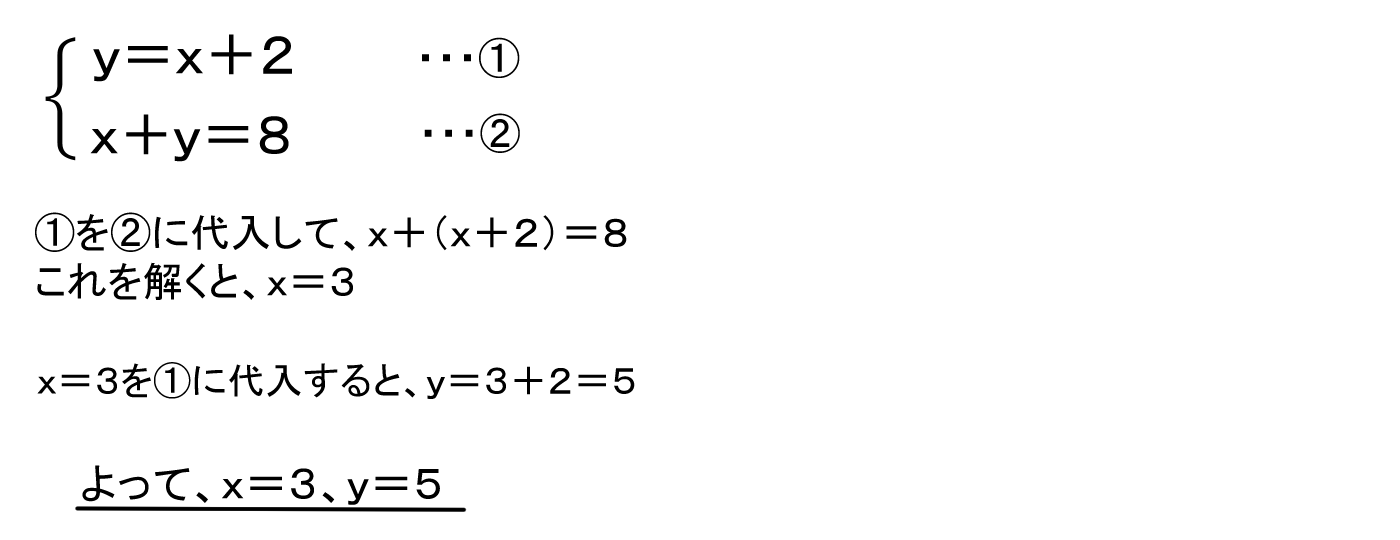


連立方程式 1 代入法と加減法 バカでもわかる 中学数学



連立方程式の2つの解き方 代入法 加減法 数学fun


分数のある連立方程式の代入法の解き方


第1章 連立方程式



連立二元一次方程式をいろいろな方法で解いてみよう 身勝手な主張



連立方程式代入法の悩みどころ 自習空間のブログ



連立方程式 代入法 計算ドリル 問題集 数学fun
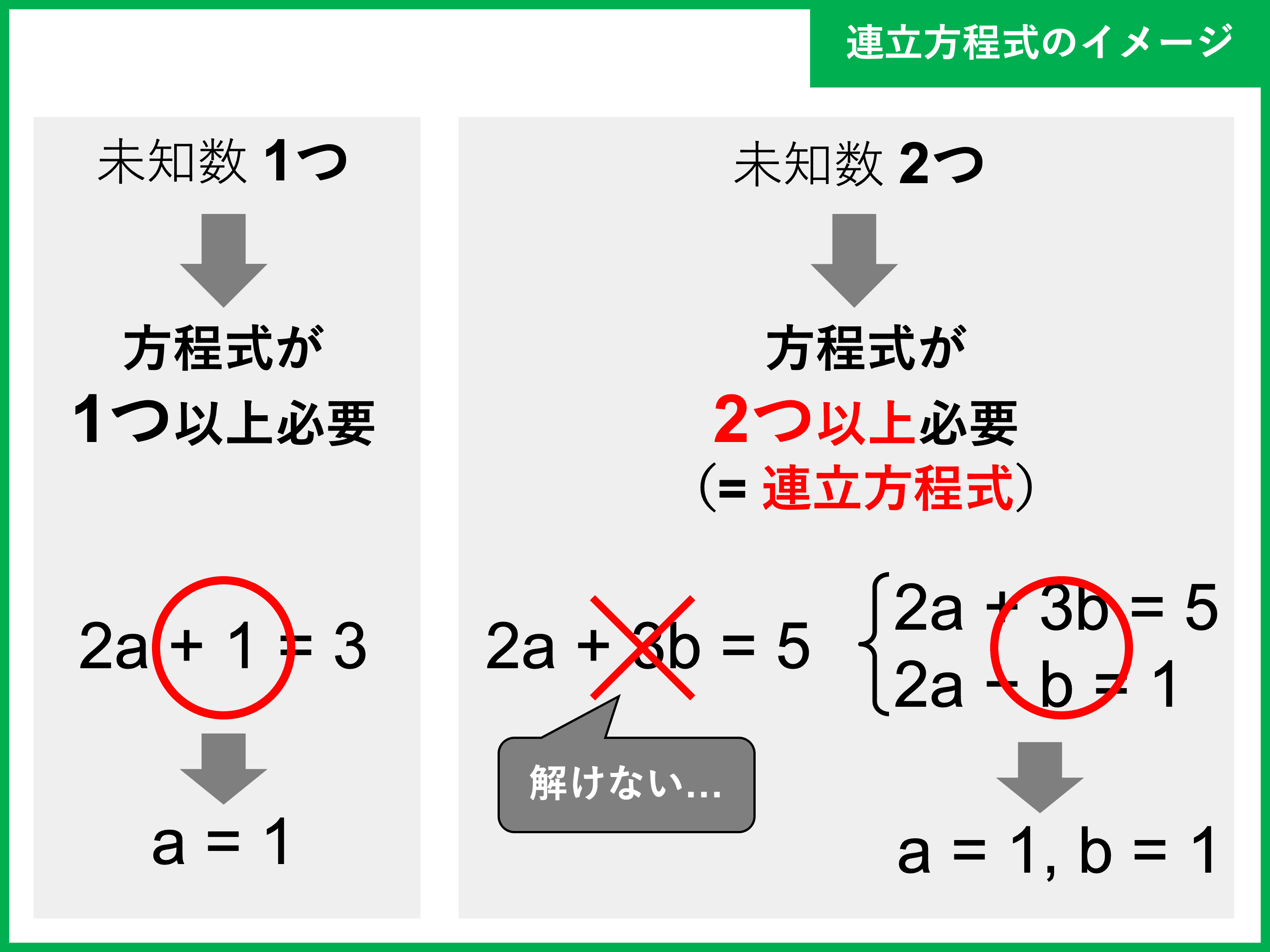


連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典



連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学
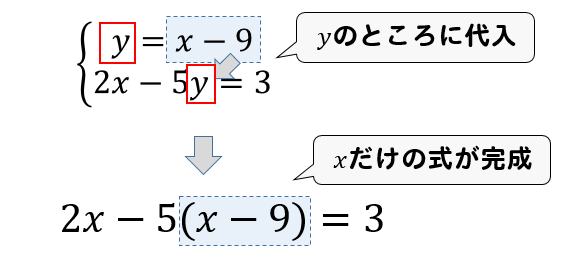


連立方程式 代入法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト


連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料


中2第2章24連立方程式とその解き方 代入法 中学数学 1学期


連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料



連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



数学 中2 17 連立方程式 代入法編 Youtube


連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
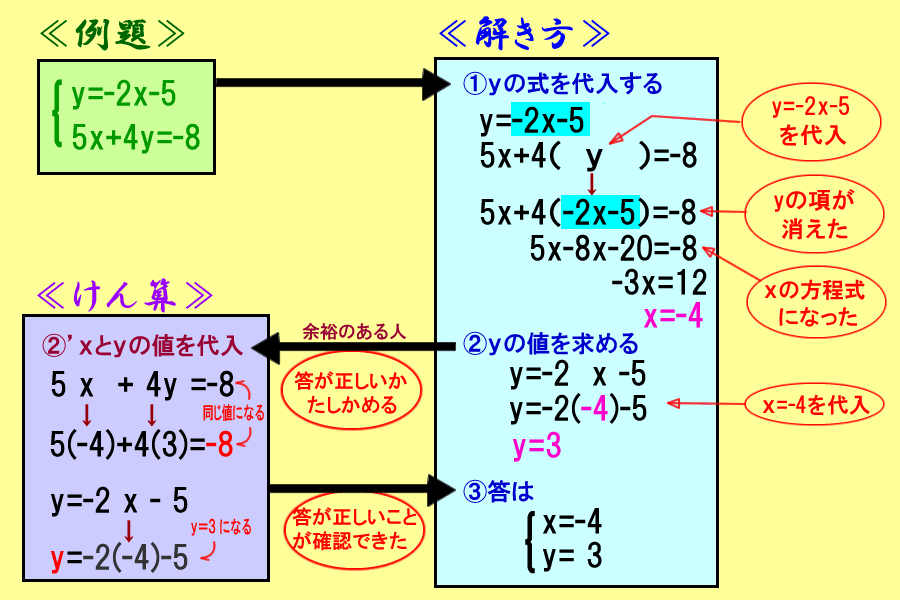


中学2年 数学 連立方程式 解き方 代入法 標準問題



連立方程式の解き方 代入法



解き方 連立方程式の加減法がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



連立方程式の解き方 代入法 苦手な数学を簡単に


代入法とは 1分でわかる意味 連立方程式の解き方 代入法のやり方 移項 加減法との関係


中2 連立方程式の 代入法 と 加減法 中学数学の方程式 中間 期末テスト 高校入試対策



毎日計算練習問題 連立方程式15 滋賀大学受験対策専門数学塾 安澤数学教室



連立方程式 1 代入法と加減法 バカでもわかる 中学数学



中学数学 連立方程式 代入法 中学数学の無料オンライン学習サイトchu Su


Studydoctor連立方程式の解き方 加減法 中2数学 Studydoctor
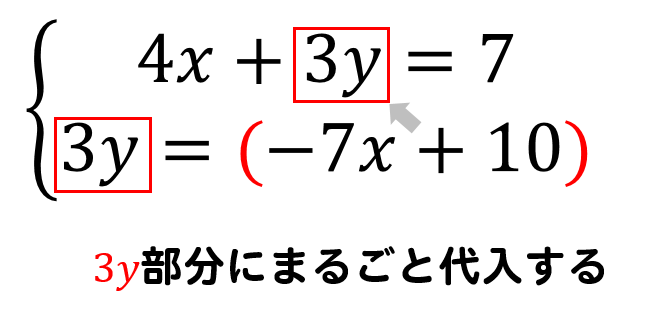


連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ



連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



2 連立方程式の解き方 代入法 やすこぶたの勉強部屋中2


連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料
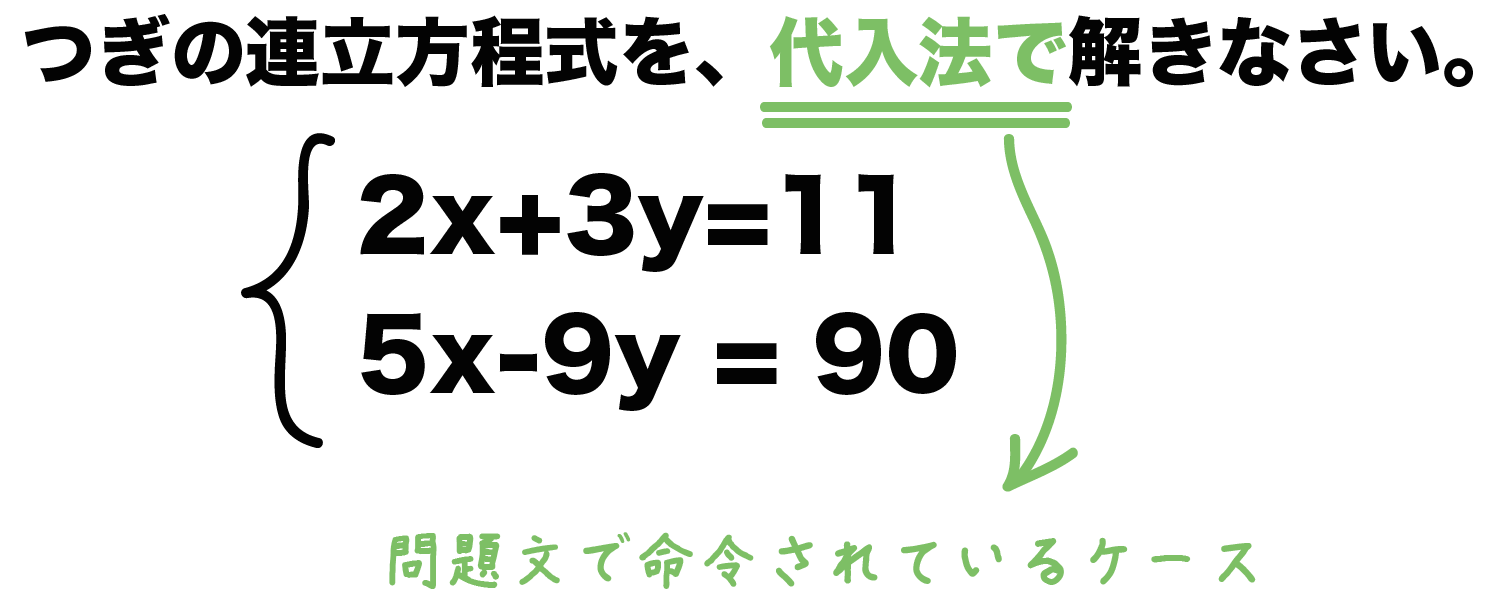


超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく



中学2年 数学 連立方程式 代入法 Youtube



中学数学 連立方程式 の効果的な教え方 代入法



中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook



連立方程式の2つの解き方 代入法 加減法 数学fun
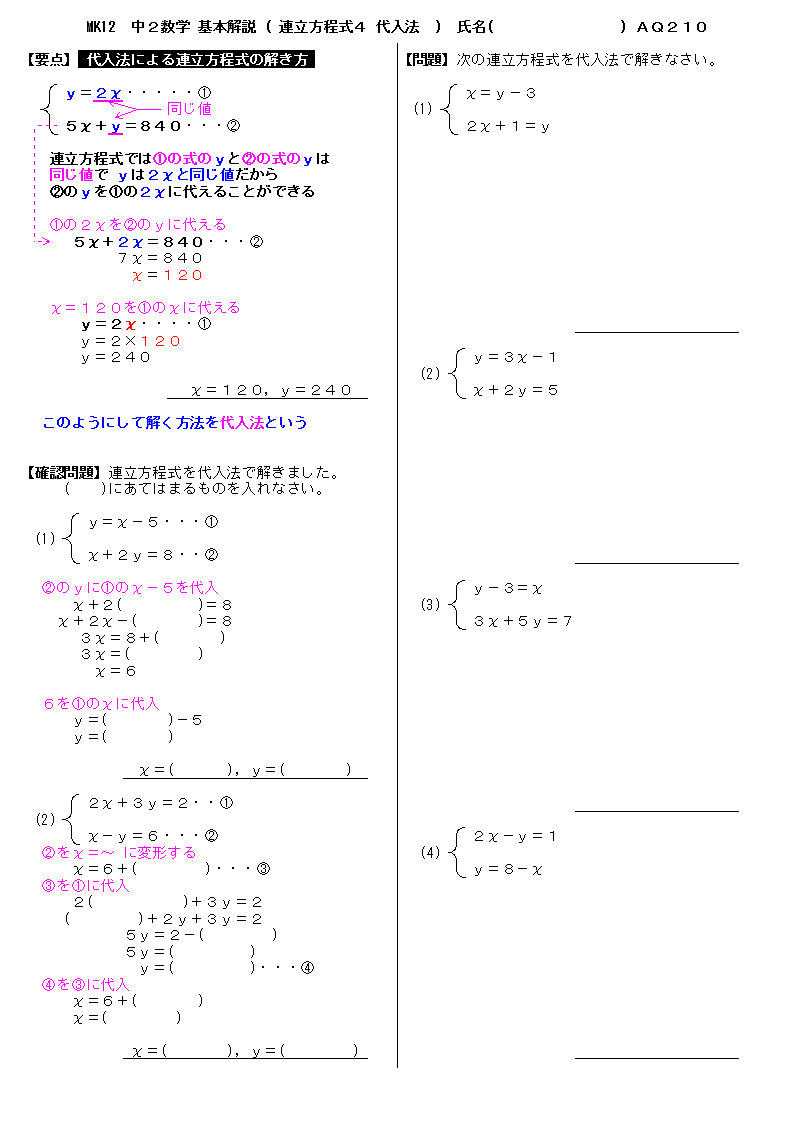


無料 中2数学 基本解説 問題プリント 210 連立方程式4 代入法



中学数学2年 連立方程式の解と係数 受験の月



0 件のコメント:
コメントを投稿